Solving a Homography problem leads to solving a set of homogeneous linear equations such below:
\begin{equation}
\left(
\begin{array}{ccccccccc}
-x1 & -y1 & -1 & 0 & 0 & 0 & x1*xp1 & y1*xp1 & xp1\\
0 & 0 & 0 & -x1 & -y1 & -1 & x1*yp1 & y1*yp1 & yp1\\
-x2 & -y2 & -1 & 0 & 0 & 0 & x2*xp2 & y2*xp2 & xp2\\
0 & 0 & 0 & -x2 & -y2 & -1 & x2*yp2 & y2*yp2 & yp2\\
-x3 & -y3 & -1 & 0 & 0 & 0 & x3*xp3 & y3*xp3 & xp3\\
0 & 0 & 0 & -x3 & -y3 & -1 & x3*yp3 & y3*yp3 & yp3\\
-x4 & -y4 & -1 & 0 & 0 & 0 & x4*xp4 & y4*xp4 & xp4\\
0 & 0 & 0 & -x4 & -y4 & -1 & x4*yp4 & y4*yp4 & yp4\\
\end{array}
\right) *H=0
\end{equation}
\( H^{*} \underset{H}{\mathrm{argmin}}= \|AH\|^{2} \) subject to \( \|H\|=1 \)
We can’t use least square since it’s a homogeneous linear equations (the other side of equation is 0 therfore we can’t just multyly it by the psudo inverse). To solve this problem we use Singular-value Decomposition (SVD).
For any given matrix \( A_{M{\times}N} \)
\begin{equation}
\underbrace{\mathbf{A}}_{M \times N} = \underbrace{\mathbf{U}}_{M \times M} \times \underbrace{\mathbf{\Sigma}}_{M\times N} \times \underbrace{\mathbf{V}^{\text{T}}}_{N \times N}
\end{equation}
\(U\) is an \( {M\times M} \) matrix with orthogonal matrix (columns are eigen vectors of A).
\(\Sigma\) is an \( {M\times N} \) matrix with non-negative entries, termed the singular values (diagonal entries are eigen values of A).
\(V \) is an \( {N\times N} \) orthogonal matrix.
\( H^{*} \) is the last column of \(V \)
Finding homography matrix in Matlab between 4 pairs of points
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
function H=homography(x1,y1,x2,y2,x3,y3,x4,y4 , xp1,yp1,xp2,yp2,xp3,yp3,xp4,yp4) %This function will find the homography betweeb 4 points using svd A=[ -x1 -y1 -1 0 0 0 x1*xp1 y1*xp1 xp1; 0 0 0 -x1 -y1 -1 x1*yp1 y1*yp1 yp1; -x2 -y2 -1 0 0 0 x2*xp2 y2*xp2 xp2; 0 0 0 -x2 -y2 -1 x2*yp2 y2*yp2 yp2; -x3 -y3 -1 0 0 0 x3*xp3 y3*xp3 xp3; 0 0 0 -x3 -y3 -1 x3*yp3 y3*yp3 yp3; -x4 -y4 -1 0 0 0 x4*xp4 y4*xp4 xp4; 0 0 0 -x4 -y4 -1 x4*yp4 y4*yp4 yp4]; [U,S,V] = svd(A); H=V(:,end); H=reshape(H,3,3); |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
%This script will find the homography between 4 points and their repsective %projection %These points are for vertex of a square in world cordinate system, the %lengh of square is 150 x0=0; y0=0; x1=150; y1=0; x2=150; y2=150; x3=0; y3=150; %The projected position of points xp0=100; yp0=100; xp1=200; yp1=80; xp2=220; yp2=80; xp3=100; yp3=200; fprintf('Estimated homography matrix is:') H=homography(x0,y0, x1,y1, x2,y2, x3,y3, xp0,yp0, xp1,yp1, xp2,yp2,xp3,yp3) p0=[x0,y0; x1,y1 ; x2,y2 ; x3,y3]; p1=[xp0,yp0; xp1,yp1; xp2,yp2; xp3,yp3]; %We project the point (x2 y2) by H and we should get (xp2 yp2) projected_point=[x2 y2 1] * H; projected_point(1,1)/projected_point(1,3) projected_point(1,2)/projected_point(1,3) |
Finding homography matrix in OpenCV between 4 pairs of points
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
void get_homographyMatrix() { std::vector<cv::Point2f> obj; std::vector<cv::Point2f> scene; std::vector<cv::Point2f> obj_projection; cv::Point2f A,B,C,D,A_P,B_P,C_P,D_P ; A.x=0; A.y=0; B.x=150; B.y=0; C.x=150; C.y=150; D.x=0; D.y=150; obj.push_back(A); obj.push_back(B); obj.push_back(C); obj.push_back(D); A_P.x=100; A_P.y=100; B_P.x=200; B_P.y=80; C_P.x=220; C_P.y=80; D_P.x=100; D_P.y=200; scene.push_back(A_P); scene.push_back(B_P); scene.push_back(C_P); scene.push_back(D_P); cv::Mat homography_matrix= cv::getPerspectiveTransform(obj,scene); std::cout<<"Estimated Homography Matrix is:" <<std::endl; std::cout<< homography_matrix <<std::endl; perspectiveTransform( obj, obj_projection, homography_matrix); for(std::size_t i=0;i<obj_projection.size();i++) { std::cout<<obj_projection.at(i).x <<"," <<obj_projection.at(i).y<<std::endl; } } |
Finding homography matrix in OpenCV between N pairs of points


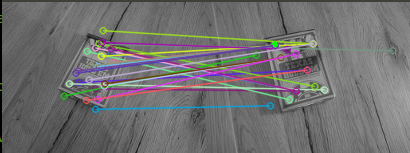
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 |
void findHomography_Test(int argc, char** argv) { // The input arrays src_points and dst_points can be either // 1)N-by-2(pixel coordinates) matrices // 2)N-by-3 (homogeneous coordinates) matrices // The final argument, homography, is just a 3-by-3 matrix to // void cvFindHomography(const CvMat* src_points, const CvMat* dst_points, CvMat* homography ); if( argc != 3 ) { printf(" Usage: ./main_Homography <img1> <img2>\n"); return; } Mat img_object = imread( argv[1], CV_LOAD_IMAGE_GRAYSCALE ); Mat img_scene = imread( argv[2], CV_LOAD_IMAGE_GRAYSCALE ); if( !img_object.data || !img_scene.data ) { printf(" --(!) Error reading images \n"); return ; } //-- Step 1: Detect the keypoints using SURF Detector int minHessian = 400; SurfFeatureDetector detector( minHessian ); std::vector<KeyPoint> keypoints_object, keypoints_scene; detector.detect( img_object, keypoints_object ); detector.detect( img_scene, keypoints_scene ); //-- Step 2: Calculate descriptors (feature vectors) SurfDescriptorExtractor extractor; Mat descriptors_object, descriptors_scene; extractor.compute( img_object, keypoints_object, descriptors_object ); extractor.compute( img_scene, keypoints_scene, descriptors_scene ); //-- Step 3: Matching descriptor vectors using FLANN matcher FlannBasedMatcher matcher; std::vector< DMatch > matches; matcher.match( descriptors_object, descriptors_scene, matches ); double max_dist = 0; double min_dist = 100; //-- Quick calculation of max and min distances between keypoints for( int i = 0; i < descriptors_object.rows; i++ ) { double dist = matches[i].distance; if( dist < min_dist ) min_dist = dist; if( dist > max_dist ) max_dist = dist; } printf("-- Max dist : %f \n", max_dist ); printf("-- Min dist : %f \n", min_dist ); //-- Draw only "good" matches (i.e. whose distance is less than 3*min_dist ) std::vector< DMatch > good_matches; for( int i = 0; i < descriptors_object.rows; i++ ) { if( matches[i].distance < 1.5*min_dist ) { good_matches.push_back( matches[i]); } } Mat img_matches; drawMatches( img_object, keypoints_object, img_scene, keypoints_scene, good_matches, img_matches, Scalar::all(-1), Scalar::all(-1), vector<char>(), DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS ); //-- Localize the object from img_1 in img_2 std::vector<Point2f> obj; std::vector<Point2f> scene; for( size_t i = 0; i < good_matches.size(); i++ ) { //-- Get the keypoints from the good matches obj.push_back( keypoints_object[ good_matches[i].queryIdx ].pt ); scene.push_back( keypoints_scene[ good_matches[i].trainIdx ].pt ); } Mat H = findHomography( obj, scene, CV_RANSAC ); //-- Get the corners from the image_1 ( the object to be "detected" ) std::vector<Point2f> obj_corners(4); obj_corners[0] = Point(0,0); obj_corners[1] = Point( img_object.cols, 0 ); obj_corners[2] = Point( img_object.cols, img_object.rows ); obj_corners[3] = Point( 0, img_object.rows ); std::vector<Point2f> scene_corners(4); perspectiveTransform( obj_corners, scene_corners, H); //-- Draw lines between the corners (the mapped object in the scene - image_2 ) Point2f offset( (float)img_object.cols, 0); line( img_matches, scene_corners[0] + offset, scene_corners[1] + offset, Scalar(0, 255, 0), 4 ); line( img_matches, scene_corners[1] + offset, scene_corners[2] + offset, Scalar( 0, 255, 0), 4 ); line( img_matches, scene_corners[2] + offset, scene_corners[3] + offset, Scalar( 0, 255, 0), 4 ); line( img_matches, scene_corners[3] + offset, scene_corners[0] + offset, Scalar( 0, 255, 0), 4 ); //-- Show detected matches imshow( "Good Matches & Object detection", img_matches ); waitKey(0); return ; } |
Applying homography matrix in OpenCV



|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 |
// We need 4 corresponding 2D points(x,y) to calculate homography. vector<Point2f> left_image; // Stores 4 points(x,y) of the logo image. Here the four points are 4 corners of image. vector<Point2f> right_image; // stores 4 points that the user clicks(mouse left click) in the main image. // Image containers for main and logo image Mat imageMain; Mat imageLogo; // Function to add main image and transformed logo image and show final output. // Icon image replaces the pixels of main image in this implementation. void showFinal(Mat src1,Mat src2) { Mat gray,gray_inv,src1final,src2final; cvtColor(src2,gray,CV_BGR2GRAY); threshold(gray,gray,0,255,CV_THRESH_BINARY); //adaptiveThreshold(gray,gray,255,ADAPTIVE_THRESH_MEAN_C,THRESH_BINARY,5,4); bitwise_not ( gray, gray_inv ); src1.copyTo(src1final,gray_inv); src2.copyTo(src2final,gray); Mat finalImage = src1final+src2final; namedWindow( "output", WINDOW_AUTOSIZE ); imshow("output",finalImage); cvWaitKey(0); } // Here we get four points from the user with left mouse clicks. // On 5th click we output the overlayed image. void on_mouse( int e, int x, int y, int d, void *ptr ) { if (e == EVENT_LBUTTONDOWN ) { if(right_image.size() < 4 ) { right_image.push_back(Point2f(float(x),float(y))); cout << x << " "<< y <<endl; } else { cout << " Calculating Homography " <<endl; // Deactivate callback cv::setMouseCallback("Display window", NULL, NULL); // once we get 4 corresponding points in both images calculate homography matrix Mat H = findHomography( left_image,right_image,0 ); Mat logoWarped; // Warp the logo image to change its perspective warpPerspective(imageLogo,logoWarped,H,imageMain.size() ); showFinal(imageMain,logoWarped); } } } /* How to run: ./main ../images/homography/main.jpg ../images/homography/logo.jpg */ int homographyPerspective_Test( int argc, char** argv ) { // We need tow argumemts. "Main image" and "logo image" if( argc != 3) { cout <<" Usage: error" << endl; return -1; } // Load images from arguments passed. imageMain = imread(argv[1], CV_LOAD_IMAGE_COLOR); imageLogo = imread(argv[2], CV_LOAD_IMAGE_COLOR); // Push the 4 corners of the logo image as the 4 points for correspondence to calculate homography. left_image.push_back(Point2f(float(0),float(0))); left_image.push_back(Point2f(float(0),float(imageLogo.rows))); left_image.push_back(Point2f(float(imageLogo.cols),float(imageLogo.rows))); left_image.push_back(Point2f(float(imageLogo.cols),float(0))); namedWindow( "Display window", WINDOW_AUTOSIZE );// Create a window for display. imshow( "Display window", imageMain ); setMouseCallback("Display window",on_mouse, NULL ); // Press "Escape button" to exit while(1) { int key=cvWaitKey(10); if((char)key==(char)27) break; } return 0; } |
do you do home works for students
No sorry, got no free time 🙂
can you do a video on the mathematics for “what is SVD” as well? you seem to have a good grasp on mathematics.