Silhouette coefficient is another method to determine the optimal number of clusters. Here I introduced c-index earlier. The silhouette coefficient of a data measures how well data are assigned to its own cluster and how far they are from other clusters. A silhouette close to 1 means the data points are in an appropriate cluster and a silhouette coefficient close to −1 implies out data is in the wrong cluster. The following is python code for computing the coefficient and plotting number fo clusters vs Silhouette coefficient.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
from sklearn import cluster import numpy as numpy import sklearn import matplotlib.pyplot as plt obs = numpy.concatenate( (numpy.random.randn(100, 2) , 20 + numpy.random.randn(300, 2) , -15+numpy.random.randn(200, 2))) silhouette_score_values=list() NumberOfClusters=range(2,30) for i in NumberOfClusters: classifier=cluster.KMeans(i,init='k-means++', n_init=10, max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True) classifier.fit(obs) labels= classifier.predict(obs) print "Number Of Clusters:" print i print "Silhouette score value" print sklearn.metrics.silhouette_score(obs,labels ,metric='euclidean', sample_size=None, random_state=None) silhouette_score_values.append(sklearn.metrics.silhouette_score(obs,labels ,metric='euclidean', sample_size=None, random_state=None)) plt.plot(NumberOfClusters, silhouette_score_values) plt.title("Silhouette score values vs Numbers of Clusters ") plt.show() Optimal_NumberOf_Components=NumberOfClusters[silhouette_score_values.index(max(silhouette_score_values))] print "Optimal number of components is:" print Optimal_NumberOf_Components |
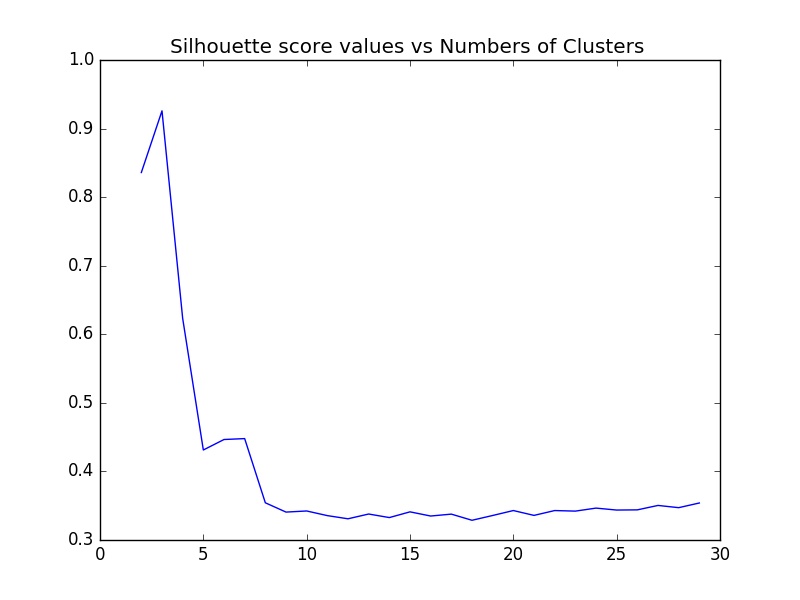
[…] Here there is also another method called “Silhouette coefficient” for finding the optimal number of components for clustering. […]