There are several approaches for estimating the probability distribution function of a given data:
1)Parametric
2)Semi-parametric
3)Non-parametric
A parametric one is GMM via algorithm such as expectation maximization. Here is my other post for expectation maximization.
Example of Non-parametric is the histogram, where data are assigned to only one bin and depending on the number bins that fall within an interval the height of histogram will be determined.
Kernel Density Estimation (KDE) is an example of a non-parametric method for estimating the probability distribution function. It is very similar to histogram but we don’t assign each data to only to a bin. In KDE we use a kernel function which weights data point, depending on how far are they from the point \( x \).
\begin{equation}
\hat{f}(x) = \frac{1}{nh} \sum_{i=1}^n k\bigg(\frac{ x-x_i }{h}\bigg)
\end{equation}
where \( h \) is a bandwidth parameter and \( k \) is the kernel function. One choice for kernel function is the Gaussian (normal distribution) but there are other kernel functions (uniform, triangular, biweight, triweight, Epanechnikov) that can be used as well. Choosing too small or too bog values for bandwidth might overfit or under fit our estimation. A rule of thumb for choosing bandwidth is Silverman rule.
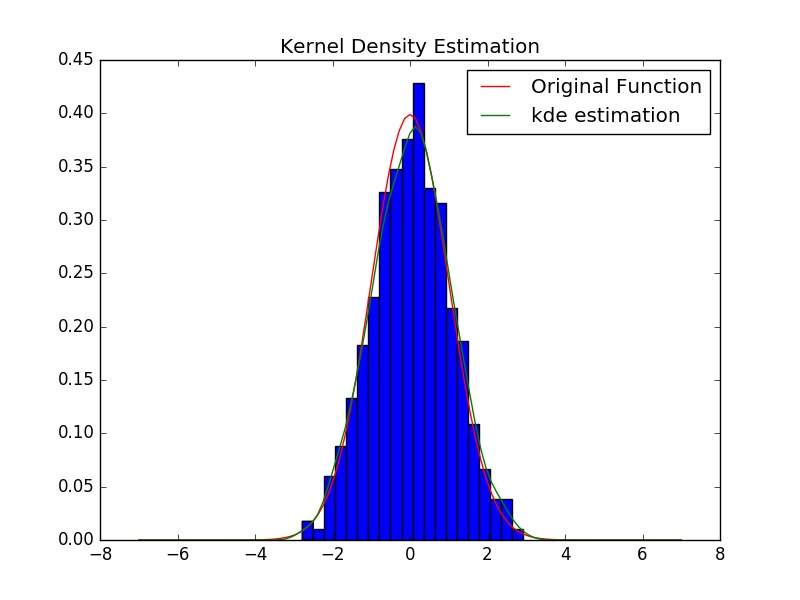
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import numpy as np from scipy import stats import matplotlib.pylab as plt n_basesample = 1000 np.random.seed(234234) xn = np.random.randn(n_basesample) gkde=stats.gaussian_kde(xn) ind = np.linspace(-7,7,101) kdepdf = gkde.evaluate(ind) plt.figure() # plot histgram of sample plt.hist(xn, bins=20, normed=1) # plot data generating density plt.plot(ind, stats.norm.pdf(ind), color="r", label='Original Function') # plot estimated density plt.plot(ind, kdepdf, label='kde estimation', color="g") plt.title('Kernel Density Estimation') plt.legend() plt.show() |