\( \)
This module finds the optimal number of components (number of clusters) for a given dataset.
In order to find the optimal number of components for, first we used k-means algorithm
with a different number of clusters, starting from 1 to a fixed max number. Then we checked the cluster validity by deploying \( C-index \) algorithm and select the optimal number of
clusters with lowest \( C-index\). This index is defined as follows:
\begin{equation} \label{C-index}
C = \frac{S-S_{min}}{S_{max}-S_{min}}
\end{equation}
where \( S \) is the sum of distances over all pairs of patterns from the same cluster. Let \( l \)
be the number of those pairs. Then \( S_{min} \) is the sum of the l smallest distances if all
pairs of patterns are considered (i.e. if the patterns can belong to different clusters).
Similarly,\(Smax \) is the sum of the\( l\) largest distance out of all pairs. Hence a small value
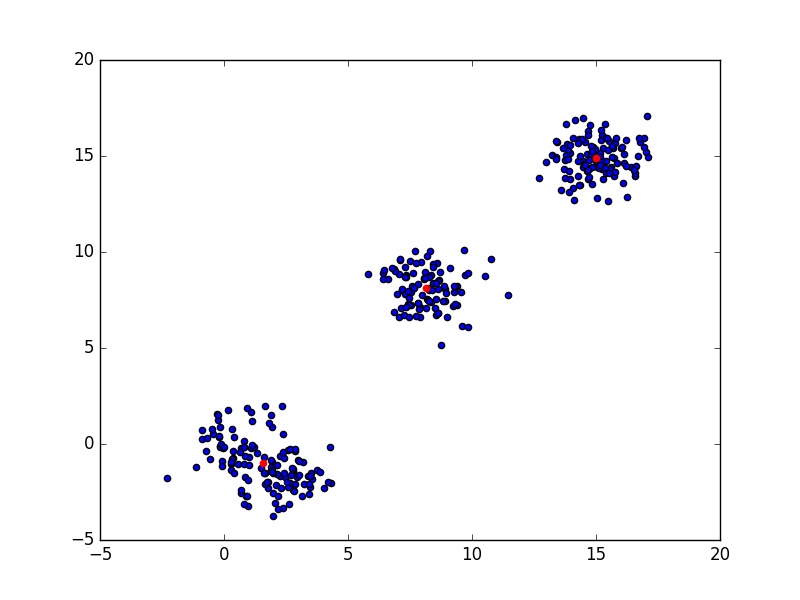
of \( C \) indicates a good clustering. In the following code, I have generated 4 clusters, but since two of them are very close, they packed into one and the optimal number of clusters is 3.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 |
import matplotlib.pyplot as pyplot import numpy as numpy from sklearn import cluster import math as math import sys from scipy.cluster.vq import vq, kmeans, whiten,kmeans2 import scipy as scipy ''' please read this documentation for more info about kmean algorithm http://docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.vq.kmeans.html#scipy.cluster.vq.kmeans http://docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.vq.kmeans2.html#scipy.cluster.vq.kmeans2 ''' def Combination(n,r): if n<r: return 0 else : return math.factorial(n)/( math.factorial(n-r) * math.factorial(r )) def GenerateData(): x1=numpy.random.randn(50,2) x2x=numpy.random.randn(80,1)+2 x2y=numpy.random.randn(80,1)-2 x2=numpy.column_stack((x2x,x2y)) x3=numpy.random.randn(100,2)+8 x4=numpy.random.randn(120,2)+15 z=numpy.concatenate((x1,x2,x3,x4)) return z def ShowDataWithOptimalCenters(Data,OptimalCenters): pyplot.scatter(Data[:,0],Data[:,1]) pyplot.scatter(OptimalCenters[:,0],OptimalCenters[:,1],color='red') pyplot.show() return def oldClusteringWithC_Index(Data,NumberOfClusters,NumberofIterationsForCindex,DistanceBetweenAllPairNodesSorted,DistanceMethod='euclidean'): NumberOfClusters=NumberOfClusters x=Data NumberofIterationsForCindex=NumberofIterationsForCindex NUmberOfNodesInTheClusters=0 D=DistanceBetweenAllPairNodesSorted OptimalCenter=[] C=1 Old_C=sys.maxint Scl=0 N=0 Smin=0 Smax=0 for NumberofIterations in xrange(NumberofIterationsForCindex): #init : {'k-means++', 'random', 'points','matrix'} #'k-means++' : selects initial cluster centers for k-mean clustering in a smart way to speed up convergence # http://scikit-learn.sourceforge.net/modules/generated/scikits.learn.cluster.KMeans.html#scikits.learn.cluster.KMeans classifier=cluster.KMeans(k=NumberOfClusters, init='random', n_init=10, max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True) y=classifier.fit(x) for i in xrange( NumberOfClusters ): # print 'NumberofIterations' # print NumberofIterations # print 'NumberOfClusters' # print NumberOfClusters # print 'classifier.cluster_centers_' # print classifier.cluster_centers_ NUmberOfNodesInTheClusters=len(x[numpy.where(classifier.labels_==i)]) Scl=Scl+numpy.sum( scipy.spatial.distance.pdist(x[numpy.where(classifier.labels_==i)], DistanceMethod)) N=N+Combination(NUmberOfNodesInTheClusters, 2) Smin=numpy.sum( D[0:N:1]) Smax=numpy.sum(D[len(D)-N::1]) if(Smax-Smin==0): continue C=(Scl-Smin)/(Smax-Smin) Scl=0 N=0 Smin=0 Smax=0 if(C<Old_C): Old_C=C OptimalCenter=classifier.cluster_centers_[:] return OptimalCenter,Old_C def ClusteringWithC_Index(Data,NumberOfClusters,NumberofIterationsForCindex,DistanceBetweenAllPairNodesSorted,DistanceMethod='euclidean'): NumberOfClusters=NumberOfClusters x=Data NumberofIterationsForCindex=NumberofIterationsForCindex NUmberOfNodesInTheClusters=0 D=DistanceBetweenAllPairNodesSorted OptimalCenter=[] C=1 Old_C=sys.maxint Scl=0 N=0 Smin=0 Smax=0 for NumberofIterations in xrange(NumberofIterationsForCindex): centroid,labels=Classifier=kmeans2(Data, NumberOfClusters, iter=500, thresh=1e-05, minit='random', missing='warn') for i in xrange( NumberOfClusters ): NUmberOfNodesInTheClusters=len(x[numpy.where(labels==i)]) Scl=Scl+numpy.sum( scipy.spatial.distance.pdist(x[numpy.where(labels==i)], DistanceMethod)) N=N+Combination(NUmberOfNodesInTheClusters, 2) Smin=numpy.sum( D[0:N:1]) Smax=numpy.sum(D[len(D)-N::1]) if(Smax-Smin==0): continue C=(Scl-Smin)/(Smax-Smin) Scl=0 N=0 Smin=0 Smax=0 if(C<Old_C): Old_C=C OptimalCenter=centroid[:] return OptimalCenter,Old_C Data=GenerateData() NumberofIterationsForCindex=50 DistanceMethod='euclidean' MaxNumberOfClusters=20 ListOfCindexes=[] ListOfCenters=[] MinimumOfCindexes=[] CentersForCurrentCluster=[] CindexForCurrentCluster=0 DistanceBetweenAllPairNodes = scipy.spatial.distance.pdist(Data, DistanceMethod) DistanceBetweenAllPairNodesSorted= numpy.sort(DistanceBetweenAllPairNodes) for NumberOfClusters in numpy.arange(1,MaxNumberOfClusters,1): CentersForCurrentCluster,CindexForCurrentCluster =ClusteringWithC_Index(Data, NumberOfClusters,NumberofIterationsForCindex,DistanceBetweenAllPairNodesSorted,DistanceMethod) ListOfCenters.append(CentersForCurrentCluster[:]) ListOfCindexes.append(CindexForCurrentCluster) IndexOfOptimalNumberOfComponents=numpy.argmin(ListOfCindexes) Centers=ListOfCenters[IndexOfOptimalNumberOfComponents] pyplot.figure() pyplot.scatter(Data[:,0], Data[:,1]) pyplot.scatter( Centers[:,0], Centers[:,1],color='red') pyplot.show() print Centers |
Here there is also another method called “Silhouette coefficient” for finding the optimal number of components for clustering.
[…] coefficient is another method to determine the optimal number of clusters. Here I introduced Cluster validation earlier. The silhouette coefficient of a data measures how well […]